POST2 - A cộng B version 2

Cho 3 dãy N số nguyên A1, A2, ..., An, B1, B2, ..., Bn và C1, C2, ..., Cn. Hãy đếm số bộ 3 (Ai,Bj,Ck) thỏa mãn Ai + Bj = Ck.

Input

 - Dòng đầu ghi số N. ( N <= 10⁵ )
 - Dòng thứ 2 ghi N số nguyên có giá trị tuyệt đối không vượt quá 50000 thể hiện dãy A.
 - Dòng thứ 3 và thứ 4 lần lượt ghi dãy B và C theo quy cách tương tự.

Output

 - Số bộ 3 thỏa mãn.

Example

Input:
3
-1 1 1
-1 2 3
2 3 -2

Output:
4

Thời gian chạy:	0.25s
Giới hạn mã nguồn:	50000B
Memory limit:	1536MB

Thuật toán

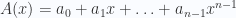 - Nhận xét: Cho 2 đa thức và 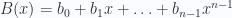, tính đa thức 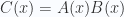. Nghĩa là tìm các hệ số 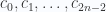của đa thức 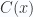(Do 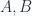  có bậc 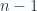nên 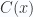có bậc lớn nhất là ).
Công thức của các hệ số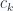 là

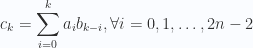
trong đó nếu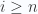 ta đặt 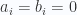. Như vậy, để tính tất cả các hệ số của đa thức 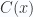bằng công thức trên ta cần 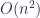phép tính. Tuy nhiên, ta có thể tính các hệ số của đa thức 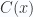chỉ với độ phức tạp 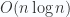bằng phép biến đổi Fourier nhanh (Fast Fourier Transform – FFT). (tham khảo)

-  Bây giờ ta biểu diễn dãy số a[i] thành dạng đa thức có bậc:
ví dụ: A={1,2,3} thành $ \color{green} f(x)=x^1+x^2+x^3 $
hoặc: B={2,3,3,4} thành g(x)=x^2+2x^3+x^4 ....
Khi nhân f(x) với g(x) ta quan tâm đến số mũ. Đó chính là tổng $ \color{green} Ai+Bj$.

Mã nguồn:

- ideone.com
- github.com

 

Read More

NK05EOPR - Đổi chỗ

Bài toán

Cho một dãy số là một hoán vị của 12 số tự nhiên đầu tiên (từ 0 đến 11). Giả sử số 0 ở vị trí thứ i trong dãy số (vị trí được đánh số từ 0 đến 11, từ trái sang phải) thì bạn có thể đổi chỗ số 0 với số ở vị trí thứ j nếu thỏa mãn cả hai điều kiện sau:

• | i – j | = d_k , với k=1..3 và (d₁,d₂,d₃,d₄)=(1;3;6;12)
• [i/d_k+1]=[j/d_k+1], với [] là hàm phần nguyên

Bạn hãy tìm số phép đổi chỗ ít nhất để có thể sắp xếp dãy số theo thứ tự tăng dần

Dữ liệu vào

Dòng đầu tiên là một số nguyên t cho biết số lượng test (t<=20)
Mỗi bộ test bao gồm một dòng là dãy bao gồm các số từ 0 đến 11, mỗi số ngăn cách bởi một khoảng trắng.
Biết rằng mỗi dãy số cho trước luôn luôn có thể sắp xếp tăng dần bằng phép đổi chỗ đã quy định

Kết qủa

Với mỗi bộ test, in ra số phép đổi chỗ ít nhất để sắp xếp dãy số đã cho theo thứ tự tăng dần

Ví dụ

Input
2
1 10 2 3 0 5 7 4 8 6 9 11
6 4 1 0 3 5 9 7 2 10 11 8

Output
8
9

Giới hạn

Thời gian chạy:	18s
Giới hạn mã nguồn:	50000B
Memory limit:	1536MB

Giải thuật

- Thuật toán A*

Mã nguồn

- ideone.com
- github.com

Read More

NK05DSRT - Sa mạc

Bài toán

Bờm vô tình bị lạc vào trong 1 ốc đảo có 1 bộ tộc thổ dân sinh sống trong 1 lần đi qua sa mạc. Bờm muốn thoát khỏi sa mạc để về nhà. Người thổ dân đã cho anh một bản đồ vùng sa mạc này.

Sa mạc gồm N ốc đảo, M đường đi an toàn nối với nhau và tại mỗi ốc đảo lại có 1 hồ chứa nước rất lớn và nước chứa trong các hồ này không bao giờ cạn. Tuy nhiên hiện tại, không có nước trong các hồ.
Giả sử: Bờm đang ở ốc đảo 1, về để về đến nhà thì Bờm phải đi đến ốc đảo N. Người thổ dân cho biết rằng tại vùng sa mạc này, nếu Bờm đi đoạn đường có độ dài là L, thì Bờm phải mang uống đủ lượng nước là L, bằng không Bờm sẽ chết. Từ đó, người thổ dân đã chỉ cho Bờm cách có thể về nhà: Bờm phải vận chuyển nước từ ốc đảo 1 đển tích trữ trong các hồ tại những ốc đảo khác bằng các con đường an toàn đã có, từ đó anh có thể về nhà. Tuy nhiên, lại có 1 khó khăn khác là: trong bất cứ thời gian nào, Bờm không thể mang lượng nước quá C (do thể lực có hạn ^_^).

Yêu cầu: Hãy tìm cách giúp Bờm về nhà nhưng đồng thời sử dụng ít nước nhất (do trong sa mạc, nước rất quí !!!!)

Dữ liệu vào

Dòng đầu tiên gồm một số nguyên t cho biết số lượng test, mỗi test có dạng như sau:

• Dòng đầu tiên là 3 số nguyên N M C ngăn cách nhau bởi khoảng trắng
• M dòng tiếp theo mỗi dòng gồm 3 số nguyên I J L với y nghĩa có đường đi từ ốc đảo I đến ốc đảo J và ngược lại là an toàn và có độ dài L.

Kết qủa

Với mỗi bộ test xuất ra đúng 1 số nguyên chỉ lượng nước ít nhất cần dùng.

Giới hạn

• 1 <= N, M, C <= 200
• 1 <= L <= 30,000 
• Thời gian chạy: 1 giây
• Giới hạn mã nguồn: 5000B
• Bộ nhớ:  1536MB
• Kết quả không quá giới hạn của longint trong pascal và int trong C++

Ví dụ

Input
1
9 10 25 
1 2 3 
2 3 12 
3 4 4 
3 5 9 
4 9 13 
5 9 5 
2 6 10 
6 7 10 
7 8 10 
8 9 10 

Output
65 

Giải thích

Mang 25 nước từ 1 đến 2 sau đó lại quay về 1. Do đó, tại 2 có 19 nước. (Bờm đã uống hết (3 + 3) nước trong lần đi và về, (19 = 25 – 3 – 3)).
Lặp lại như thế 1 lần nữa, Bờm đã mang đến 2 thêm 19 nước. Sau đó lại từ 1, Bờm mang theo 15 nước đến 2. Vậy khi đến 2, Bờm có tại đây (19+19+12 = 50) nước.
Tiếp theo, Bờm lại mang 25 nước đi từ 2 đến 3, rồi quay về 2, như vậy, tại 3 có (25 – 12 – 12 = 1) nước. Từ 2, Bờm mang 25 nước còn lại đi đến 3. Tại 3, Bờm có được (1+(25-12) = 14) nước.
Cuối cùng, Bờm mang 14 nước đi đến 5 rồi đến 9. Vậy là Bờm đã thoát khỏi sa mạc.

Giải thuật

- Sử dụng thuật toán tìm đường đi có trọng số nhỏ nhất - thuật toán Dijkstra
- Ta sẽ tìm đường đi từ đỉnh N về đỉnh 1
- Khi đang xét đỉnh u, ta tìm các đỉnh kề với u (gọi là v) và tìm lượng nước nhỏ nhất cần có ở v để có thể mang được tới u. Nếu sức mang của Bờm không đủ (C<L+lượng nước cần ở đỉnh u) thì Bờm phải đi về lấy thêm cho đến khi nào đủ. Nếu C<=2*L thì Bờm không thể có nước để tích trữ, coi như không có cạnh nối hai điểm này.

Mã nguồn

- ideone.com
- github.com 

Read More

CTAIN - Containers

Problem

We are given n containers, where 1 <= n <= 4. At the beginning all of them are full of water. The liter capacity of the i-th container is a natural number o_i satisfying inequalities 1 <= o_i <= 49.
Three kinds of moves can be made:  

1. Pouring the whole content of one container into another. This move can be made unless there is too little room in the second container. 
2. Filling up one container with part of the water from another one.
3. Pouring away the whole content of one container into a drain.
   

 

 Task

Write a program that for each test case:

• Reads the number of containers n, the capacity of each container and the requested final amount of water in each container.
• Verifies, whether there exist a series of moves which leads to the requested final situation, and if there is one, the program computes the minimal number of moves leading to the requested situation,
• Writes the result. The result should be the minimal number of moves leading to the requested final situation, or one word "NO" if there is no such a sequence of moves.

Input

One integer in the first line, stating the number of test cases, followed by a blank line. There will be not more than 20 tests.
For each test case, at the first line, one positive integer n is written, n <= 4, this is the number of containers. There are n positive integers written in the second line. These are the capacities of the containers (the i-th integer o_i denotes the capacity if the i-th  container,1 <= o_i <= 49). In the third line there are written n numbers. These are the requested final volumes of water in the containers (the i-th integer w_i denotes the requested final volume of water in the i-th container, 0 <= w_i <= o_i). All integers in the second and the third line are separated by single spaces.
The test cases will be separated by a single blank line.

Output

For each test case : write one integer - the minimal number of moves which lead to the requested final situation or write only one word "NO" if it is not possible to reach the requested final situation making only allowed moves.

Example

Input:
2

3
3 5 5
0 0 4

2
20 25
10 16

Output:
6
NO

Giới hạn

Thời gian chạy:	5s
Giới hạn mã nguồn:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)

Thuật toán 

- Duyệt tất cả các trạng thái của các container (nếu không có container i thì coi như sức chứa của nó là 0, và không thao tác với nó).
- Sử dụng hàng đợi để duyệt theo chiều rộng (BFS).
- Đánh dấu trạng thái đã xuất hiện trong hàng đợi hay chưa? Sử dụng mảng exist[][][][] (kiểu int8_t để khỏi gây lỗi do sử dụng quá nhiều bộ nhớ)

Sample code   

- ideone.com
- Github.com

Read More

NK05MNIM - Bốc sỏi

Bài toán

Hai bạn Nam và Mai cùng chơi một trò chơi với n đống sỏi. Luật chơi như sau:

• Hai bạn sẽ lần lượt đi. Bạn Mai là người đi trước
• Trong mỗi lượt đi, bạn đi sẽ được quyền bốc một số sỏi bất kỳ từ một đống nhất định và phải bốc tối thiểu là 1 viên sỏi.
• Bạn nào bốc phải viên sỏi cuối cùng là người thua cuộc

Bạn hãy giúp Mai xác định xem bạn ấy có thể thắng được trong trò chơi hay không

 

 Dữ liệu vào

Dòng đầu tiên chứa một nguyên t là số bộ test. Các dòng sau là t bộ test.
Mỗi bộ test bao gồm:

• Dòng đầu tiên chứa một số nguyên n (n<=100) là số đống sỏi
• Dòng thứ hai gồm n số nguyên a₁, a₂, a₃,... , a_n, ngăn cách nhau bởi một khoảng trắng. Số nguyên ai cho biết số lượng viên sỏi có trong đống thứ i (1<=a_i<=100)

Kết quả

Với mỗi bộ test, in ra 1 nếu bạn Mai thắng, -1 nếu bạn Mai thua

Ví dụ

Input
2
4
30 4 19 75
3
1 4 5


Output
1 

-1

Giới hạn

Thời gian chạy:	0.460s
Giới hạn mã nguồn:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)

Giải thuật (Thuật thắng trò chơi NIM)

- Tổng Nim của hai số a,b là a xnor b (trong C++ kí hiệu là a^b).

- Nếu số đống sỏi lẻ và mỗi đống chỉ có một viên thì người chơi trước luôn thua.

- Nếu ban đầu (a₁, a₂, a₃,... , a_n ) có tổng Nim duơng thì người chơi trước luôn thắng. (Theo định lý Bouton)

Code mẫu

- ideone.com
- github.com

Read More

NK05ORDR - Trật tự

Bài toán:

Xét các số nguyên từ 1 đế N. Các số này được sắp xếp theo thứ tự từ điển. Ví dụ với N=11, ta có dãy số sau khi sắp xếp là 1, 10, 11, 2, 3, 4, 5, 6, 7, 8, 9.
Ký hiệu Q_N,K là vị trí của số K trong dãy được sắp xếp theo cách nói trên. Ví dụ Q_11,2=4 Cho các số nguyên K và M. Hãy tìm số nguyên N nhỏ nhất thỏa mãn Q_N,K=M

 

 Dữ liệu vào

Dòng đầu tiên chứa số nguyên t cho biết số bộ test.
Mỗi bộ test bao gồm 1 dòng duy nhất chứa 2 số nguyên K và M (1<=K,M<=10⁹)

Kết quả

Với mỗi bộ test xuất ra số N, hoặc 0 nếu không tồn tại N

Ví dụ

Input
1
2 4
Output
11

Yêu cầu

Thời gian chạy:	0.374s
Giới hạn mã nguồn:	50000B
Memory limit:	1536MB
Cluster:	Cube (Intel G860)

Code mẫu: 

- ideone.com
- github.com

 

Read More